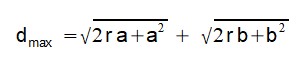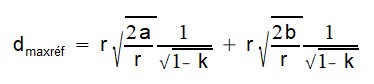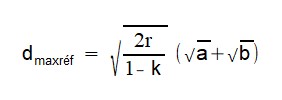La structure standard de l'atmosphère peut être considérée comme une succession de couches d'air les unes sur les autres avec, pour chacune, un indice de réfraction supérieur à celui de la couche située immédiatement au-dessus. Dans la figure 1, le cheminement réel de la lumière de l'étoile s'effectue selon le trajet issu du symbole * : au lieu de voir l'étoile dans la direction 1 en l'absence de réfraction, elle apparaît dans la direction 2, c'est-à-dire au-dessus de sa position réelle comme dans le cas d'un dioptre constitué d'une couche d'air au-dessus d'une couche d'eau (cf. page sur la présentation de la réfraction). La déviation des rayons lumineux a donc pour effet de déplacer l'image de la source un peu au-dessus de sa position géométrique réelle, qu'il s'agisse d'un objet terrestre (montagne, phare, etc.) ou extérieur à l'atmosphère (Soleil, Lune, planète, étoile). En conséquence, le Soleil et la Lune sont en réalité sous l'horizon quand ils y apparaissent tangents par leur bord inférieur.

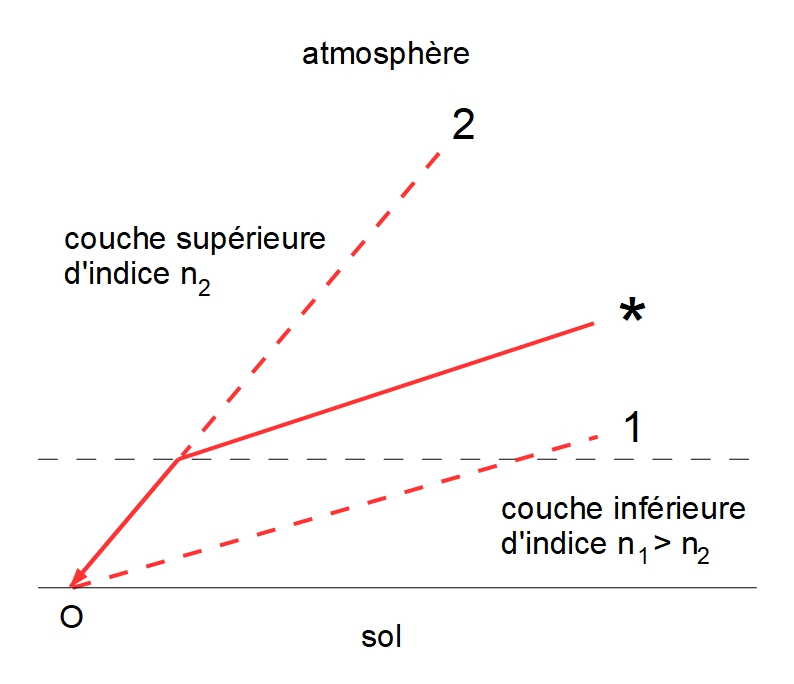
Figure 1

1. Visibilité d'une montagne grâce à la réfraction

Si, au lieu d'un objet céleste, on considère le sommet d'une montagne lointaine bien visible depuis un site d'observation, on peut déterminer si c'est grâce à la réfraction (qui élève son image) qu'il est visible. Pour cela, trois distances doivent être considérées :
- la distance réelle d entre le sommet et le site depuis lequel il est observé ;
- la distance maximale de visibilité d_max, sans considérer la réfraction, qui dépend uniquement de l'altitude des deux sites et du rayon de la Terre ;
- la distance maximale de visibilité d_maxréf en prenant en compte la réfraction (par l'intermédiaire d'un paramètre k), l'altitude des deux sites et le rayon de la Terre.

La figure 2 présente la configuration : le point d'observation est en O à l'altitude a, le sommet observé est en S1, S2 ou S3 selon la situation considérée et est à l'altitude b, C est le centre de la Terre et r son rayon. S2 correspond à la distance d_max. Si la distance d est inférieure à la distance d_max, la montagne est visible sans l'aide de la réfraction (cas S1). Si d est supérieure à d_max (cas S3), deux cas sont possibles : si d est inférieure à d_maxréf la montagne est visible grâce à l'élévation de son image par la réfraction mais si d est supérieure à d_maxréf alors la montagne est invisible car située au-delà de la limite maximale pour être visible grâce à la réfraction.

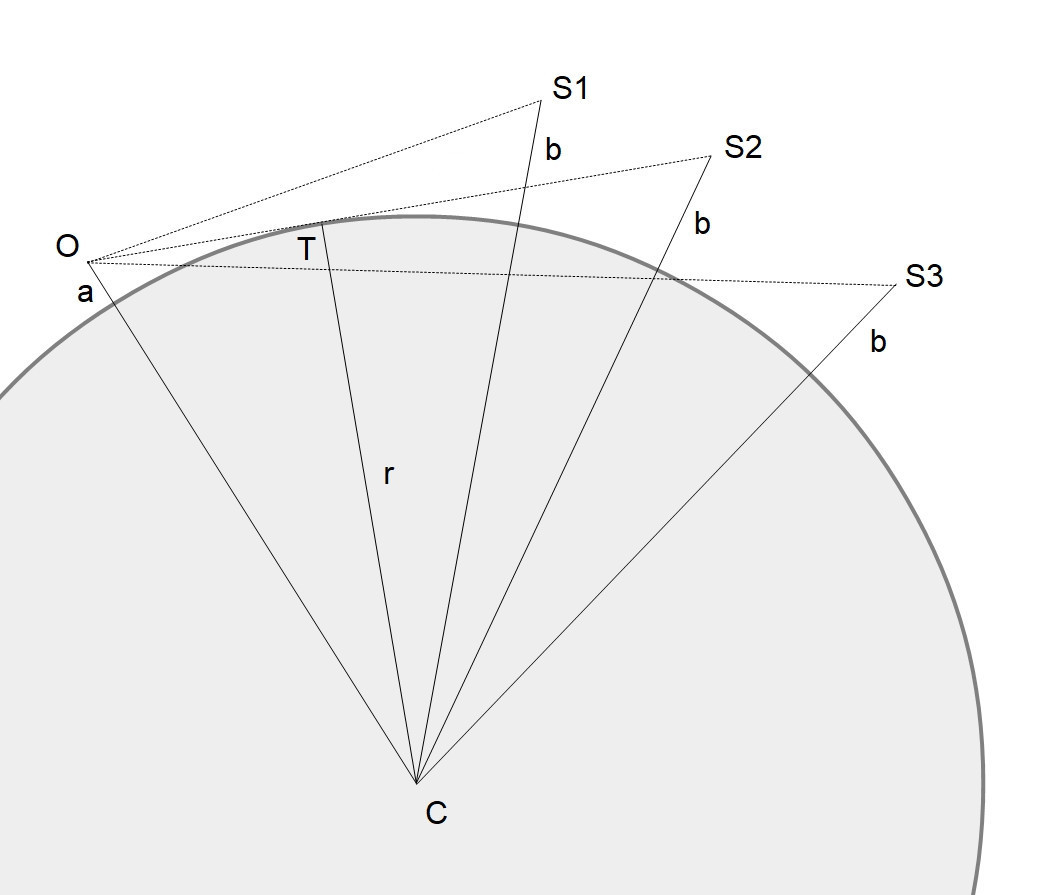
Figure 2

La distance d peut être mesurée sur une carte ou calculée selon les règles de la trigonométrie sphérique. Cette deuxième méthode est présentée dans un document de P. Rocher "Observation du Mont Canigou depuis Notre de Dame de la Garde à Marseille"¹ avec, comme intermédiaire, le calcul de la distance angulaire Δ entre les deux lieux et le calcul du rayon de la Terre r à la latitude moyenne des deux lieux. On a alors d = r Δ, avec Δ en radians.

La distance d_max est calculée simplement selon le schéma de la figure 2. C'est la distance du sommet S2 avec le segment O S2 qui correspond au trajet de la lumière en ligne droite, tangent à la surface de la Terre en T :

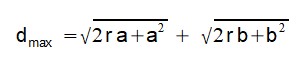
La distance d_maxréf est obtenue d'après le document de P. Rocher :

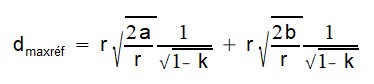
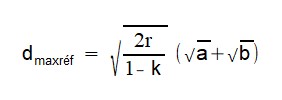
Ces trois distances sont calculées pour le sommet Asnabarra Mendia en Espagne vu depuis Biarritz à presque 100 km.

Situé au nord de Bilbao, Asnabarra Mendia est le dernier sommet avant le Cap Matxitxako, à une altitude de 434 m  ; en langue basque "mendia" signifie "la montagne". Il est indiqué par un trait blanc dans l'image 1.1 : à sa gauche, on se dirige vers le Mont Sollube (visible sur le panorama de la chaine de montagnes, cliquer sur l'image pour l'agrandir et la déplacer avec la barre horizontale qui apparaît en bas) et, à sa droite, c'est le Cap Matxitxako et l'Océan Atlantique. L'observation a été effectuée en septembre 2024 depuis l'esplanade du phare de Biarritz à l'altitude de 33 m (altitude du site + hauteur de l'appareil photographique).

Dans ces conditions, les distances sont les suivantes :
- d = 97.8 km selon les formules de P. Rocher qui prennent en compte la latitude (43.493297°) et la longitude (-1.554319°) du lieu d'observation, celles de celui observé (43.437399° et -2.76316°), avec le calcul du rayon de la Terre à leur latitude moyenne (6 376 954 m) ;
- d_max = 94.9 km, avec a = 33 m, b = 434 m et r = 6 376 954 m ;
- d_maxréf = 103.6 km avec k = 0.16.

La montagne Asnabarra est donc située à 97.8 km (d) du lieu d'observation alors que, sans réfraction, elle serait invisible au-delà de 94.9 km (d_max) qui est une distance légèrement inférieure. De plus, de façon attendue puisque la montagne est effectivement visible, la distance 97.8 km est inférieure à d_maxréf qui est égale à 103.6 km. C'est donc grâce à la réfraction qui élève son image que le sommet Asnabarra est visible depuis l'esplanade du phare de Biarritz.

2. Hauteur variable de l'image d'une montagne

Dans l'atmosphère, l'indice de réfraction dépend de la température et de la pression : d'une part, ces paramètres varient d'un jour à l'autre ainsi qu'au cours de la journée, et d'autre part, ils évoluent en fonction de l'altitude. Ainsi, lors de son trajet, l'image d'un sommet lointain va traverser une atmosphère avec une température, donc un indice de réfraction, variable en fonction du jour et de l'heure, et les montagnes apparaîtront plus ou moins hautes par rapport aux éléments d'avant-plan. De plus, en raison de la variabilité de l'indice de réfraction entre la base et le sommet de la montagne, l'image de celle-ci pourra subir une compression ou un étirement. Enfin, un effet de mirage peut s'ajouter quand le profil de température en fonction de l'altitude s'écarte fortement du taux de décroissance habituel de 6.5° C par 1000 m. En raison de ces trois effets, l'apparence d'une montagne lointaine peut varier fortement selon le jour et l'heure de son observation.

2.1 Variation absolue de la hauteur observée du Pic de Sesques

Ce phénomène de hauteur variable a été observé pour le massif de L'Escarpu (Pyrénées-Atlantiques) depuis Toulouse à 173 km. En janvier, février et juillet 2022, le Pic de Sesques (2606 m) est apparu à des hauteurs différentes au-dessus de l'horizon, plus haut en janvier (2.1) qu'en juillet (2.3) de 42".

Si on calcule la distance maximale de visibilité d_max en l'absence de réfraction, on constate qu'elle est très supérieure à la distance du Pic de Sesques : 235 km par rapport à 173 km, ce qui signifie que ce sommet serait aussi visible sans le concours de la réfraction des rayons lumineux par l'atmosphère, mais il apparaitrait un peu plus bas.

L'alignement des trois images 2.1 à 2.3 a été effectué avec des lampadaires au premier plan non montrés ici, et le sommet a été identifié grâce à un travail remarquable disponible sur http://www.webmetrue.fr/pyrenees-panorama/.

2.2 Variation relative de la hauteur observée du Mont Sollube

Pour le Mont Sollube (683 m) situé vers Bilbao (Espagne), son observation depuis Biarritz à 98 km permet de détecter la variabilité de son élévation au-dessus du niveau de l'eau. En l'absence d'élément d'avant-plan qui pourrait être considéré comme fixe malgré la réfraction, il n'est pas possible de mesurer son élévation absolue, seule la variation de celle-ci est accessible. Les images ont été alignées par rapport au niveau de l'océan, un choix arbitraire car ce niveau n'est pas identique dans toutes les images en raison de la réfraction variable et de l'effet de mirage présent ou pas. Les quatre photographies ont été effectuées exactement depuis le même emplacement à Biarritz à l'altitude de 33 m.

Dans les photographies 3.1 à 3.4, le Mont Sollube est près du bord droit avec plusieurs antennes, et le sommet à gauche est probablement le Mont Bustarrigan (561 m) situé en avant-plan. La crête sud du Mont Sollube descend vers la gauche ; elle est bien visible comme une fine bande ininterrompue dans l'image 3.2 mais elle est absente dans l'image 3.4 où les reliefs à gauche et à droite apparaissent séparés par l'océan, en raison aussi d'un faible mirage inférieur. L'image 3.3 correspond à une situation intermédiaire et, dans l'image 3.1, l'élévation au-dessus de l'océan est particulièrement importante en raison d'un étirement vertical présenté dans cette page. L'horizon optique est donc réduit dans les images 3.3 et 3.4 par rapport à 3.1 et 3.2 car les zones boisées les plus basses sont invisibles.

La hauteur du Mont Sollube mesurée au-dessus de l'eau apparaît bien différente selon les images : sa valeur la plus grande est en 3.1 (10.5') et la plus faible en 3.2 (8.2'), les images 3.3 et 3.4 étant intermédiaires (9.9').