La réfraction des rayons lumineux est un phénomène bien connu pour quiconque est entré dans une piscine avec de l'eau jusqu'à la taille car l'apparence de nos jambes (position et longueur) n'est pas celle attendue. L'explication réside dans le changement de direction d'un rayon lumineux au passage d'un dioptre, c'est-à-dire lorsque la lumière passe d'un milieu (l'eau) à un autre (l'air) avec un indice de réfraction différent.

1. La loi de Snell-Descartes

L'indice de réfraction est noté n ; il est égal à 1,33 dans l'eau et 1 dans l'air. n₁ et n₂ étant les indices de réfraction de ces deux milieux, l'angle du rayon incident i₁ est relié à celui du rayon de sortie i₂ selon la loi suivante :

Cette formule mathématique est connue comme la loi de Descartes en France et loi de Snell dans le reste du monde. Elle sera donc appelée loi de Snell-Descartes ici. Snell est un savant hollandais qui l'avait découverte quelques années avant Descartes, au début du XVII^èmesiècle.

La figure 1 ci-dessous montre le trajet de la lumière de l'eau vers l'air pour différents angles d'incidence. Celui-ci est mesuré depuis le segment O N(adir) vers la gauche (20°, 40°, etc.), et l'angle de sortie dans l'air est mesuré par rapport au segment O Z(énith) vers la droite (27°, 59°, etc.). Pour chaque angle d'incidence, les rayons incident et émergent sont figurés avec des couleurs identiques. Mais le contact d'un rayon lumineux avec le dioptre de séparation des deux milieux produit aussi un rayon réfléchi qui reste dans l'eau et se dirige vers la partie inférieure droite du schéma de façon symétrique par rapport au segment O N. Il apparaît ainsi que pour un angle d'incidence inférieur à 48.75°, le rayon incident se partage en un rayon transmis dans l'air et un autre réfléchi dans l'eau alors que, au-delà de 48.75°, seul subsiste le rayon réfléchi (comme ici le rayon d'angle d'incidence 70°). 48.75° est dénommé "angle d'incidence minimal" pour avoir une réflexion totale, sans aucun rayon réfracté.

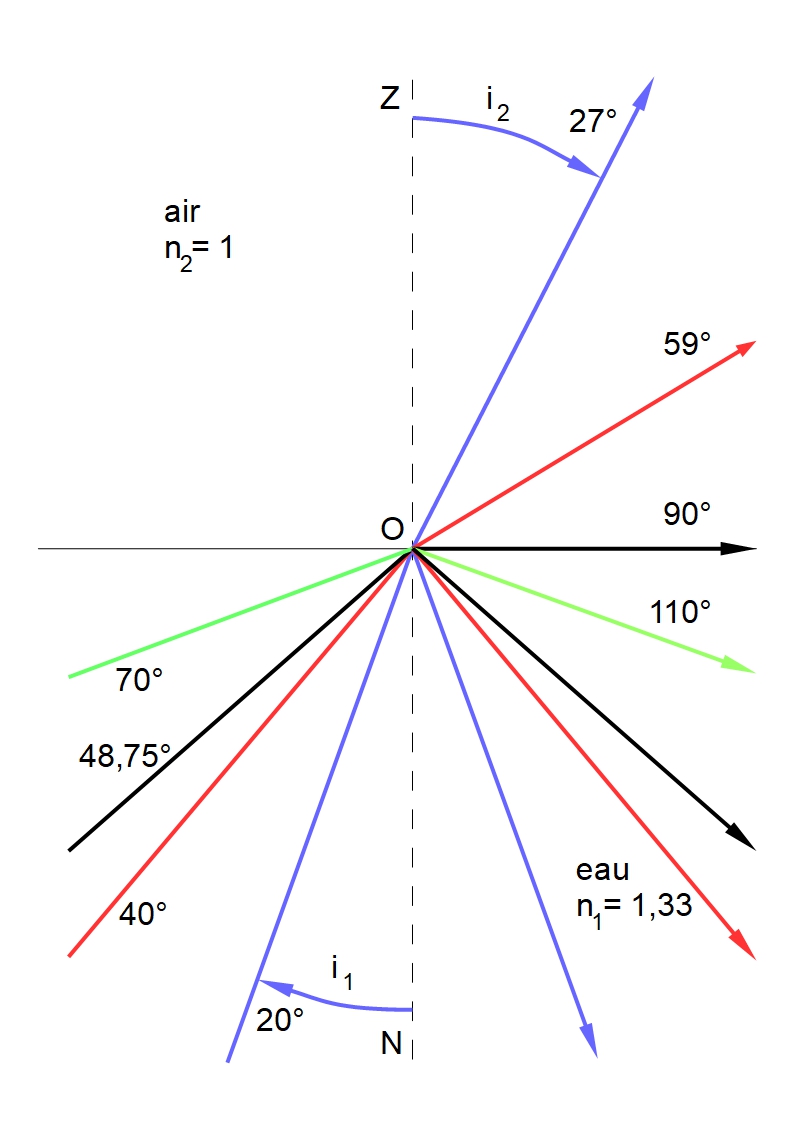Figure 1

La figure 2 montre la relation entre l'angle d'incidence i₁ (abscisse) et l'angle de sortie i₂ (ordonnée) donnée par la loi de Snell-Descartes : l'angle du rayon réfracté dans l'air est supérieur à l'angle du rayon incident dans l'eau (27° par rapport à 20° pour le rayon présenté en bleu dans la figure 1). L'angle d'incidence minimal de 48.75° est obtenu avec n₁=1.33, n₂=1 et i₂=90°.

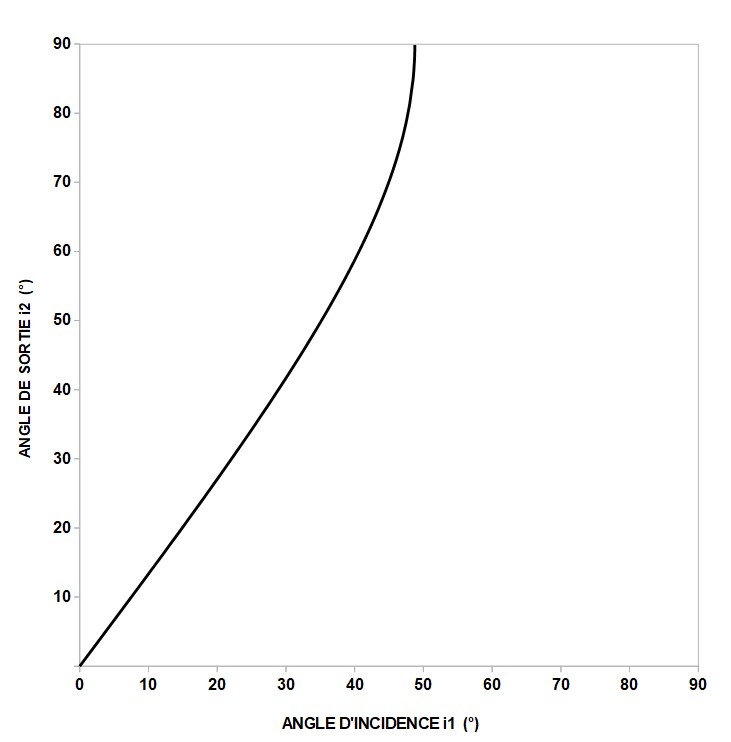Figure 2

2. L'élévation des images

On peut adapter la situation précédente pour l'appliquer à une configuration réelle dans l'atmosphère : l'air de la figure 1 devient le milieu supérieur de faible indice de réfraction et l'eau le milieu inférieur de fort indice de réfraction. Dans la figure 3, le cheminement réel de la lumière de l'étoile s'effectue selon le trajet issu du symbole * jusqu'au point d'observation O. Au lieu de voir l'étoile dans la direction 1 en l'absence de réfraction, elle apparaît dans la direction 2, c'est-à-dire au-dessus de sa position réelle. La déviation des rayons lumineux a donc pour effet de déplacer l'image de la source un peu au-dessus de sa position réelle, qu'il s'agisse d'un objet terrestre (montagne) ou extérieur à l'atmosphère (étoile, Soleil, Lune, etc.). En conséquence, le Soleil et la Lune sont en réalité sous l'horizon quand ils y apparaissent tangents par leur bord inférieur.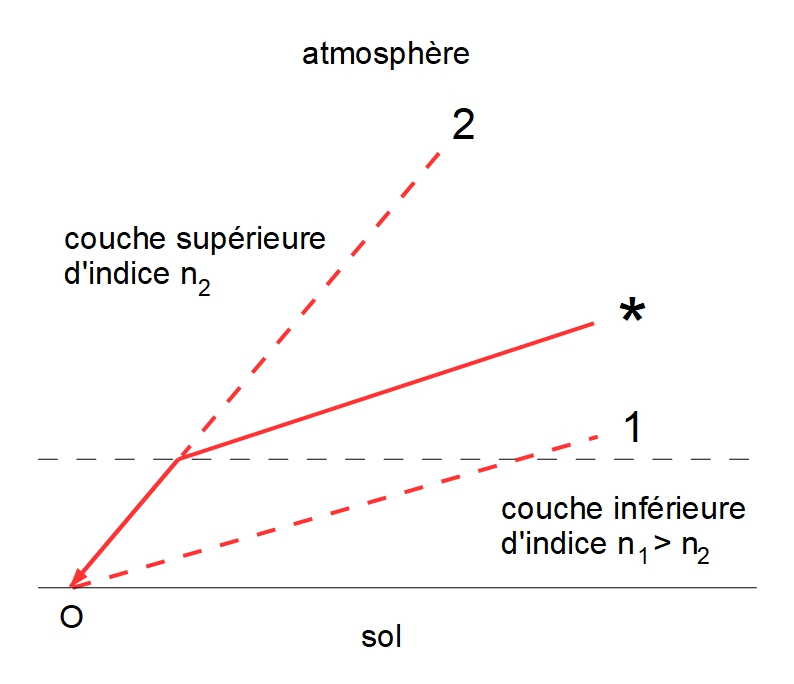

Figure 3

Si, au lieu d'un objet céleste, on considère le sommet d'une montagne lointaine bien visible depuis un site d'observation, on peut déterminer si c'est grâce à la réfraction (qui élève son image) qu'il est visible. Pour cela, deux distances doivent être considérées :
- la distance réelle d entre le sommet et le site depuis lequel il est observé ;
- la distance maximale de visibilité d_max, sans considérer la réfraction, qui dépend uniquement de l'altitude des deux sites et du rayon de la Terre.

Si la distance d est inférieure à la distance d_max, la montagne est visible sans l'aide de la réfraction. Si d est supérieure à d_max, la montagne n'est visible que grâce à l'élévation de son image par la réfraction. Un tel exemple est examiné dans la page sur l'élévation des images.

3. Compression verticale des images

Un deuxième effet s'ajoute au décalage vertical causé par la réfraction. Il est différentiel car l'amplitude de cette déviation verticale dépend de la hauteur sur l'horizon : comme l'indice de réfraction diminue quand l'altitude augmente, le décalage vertical d'une source diminue aussi quand sa hauteur sur l'horizon augmente. Avec l'exemple du Soleil proche de l'horizon, le décalage est plus important pour son bord inférieur que pour son bord supérieur. Le Soleil paraitra donc un peu aplati car le bord inférieur est plus dévié (c'est-à-dire plus relevé) que le bord supérieur (images 1.1 et 1.2).

4. Turbulences causées par la réfraction

Pour finir cette présentation, la linéarité de l'horizon marin est radicalement différente selon l'état de la réfraction juste au-dessus de l'eau : rectiligne en situation calme (image 2.1, aucun mirage) ou très perturbé, comme déchiqueté, en raison d'importantes variations locales de la réfraction (image 2.2 avec mirage inférieur ce matin-là). Cette dernière situation est encore mieux visible dans une vidéo réalisée dans les mêmes conditions. Les images 2.1 et 2.2 correspondent au même zoom optique (focale 500 mm) et au même redimensionnement (2000 pixels redimensionnés à 1000 pixels pour l'image affichée).

De façon plus générale, les turbulences causées par les variations locales rapides de la réfraction sont très communes : l'exemple le plus connu est celui d'un paysage tremblant vu au-dessus d'un feu.